Фланцы сосудов и аппаратов: конструкция и расчет прочности
Для интенсивно развивающейся химической и нефтехимической промышленности необходимо увеличение выпуска аппаратов и трубопроводов различных типоразмеров, работающих при экстремальных температурах и давлениях. При определении типоразмеров фланцев сосудов и аппаратов необходимо руководствоваться предписаниями соответствующих стандартов и алгоритмами расчета предельных нагрузок.
Дата публикации: 8 февраля 2011
Содержание
Необходимость разработки и стандартизации деталей сосудов и аппаратов
Требования на размеры фланцев сосудов и аппаратов
Оценка прочности фланца сосуда или аппарата
Расчетная схема для оценки прочности фланца
Исследование и расчет предельного напряжения фланцев сосудов и аппаратов
Алгоритм расчета фланцев сосудов и аппаратов по предельному состоянию
Необходимость разработки и стандартизации деталей сосудов и аппаратов
Для интенсивно развивающейся химической и нефтехимической промышленности необходимо увеличение выпуска аппаратов и трубопроводов различных типоразмеров, работающих при экстремальных температурах и давлениях.
В различных нормативно-технических документах указывается, как правильно производит расчет на прочность сосудов, аппаратов и деталей трубопроводов, связанных с ними, в частности, фланцев сосудов и аппаратов. Например для определения основных размеров конструктивных элементов сосудов и аппаратов высокого давления существует ГОСТ 25215-82 «Сосуды и аппараты высокого давления. Обечайки и днища. Нормы и методы расчета на прочность». Конструкции и расчет днищ, крышек, фланцев сосудов и аппаратов высокого давления, применяемых при внутреннем давлении 10…100 МПа, регламентируются также документами ОСТ 26-1046-87, ГОСТ 14249-80.
↑ В начало
Требования на размеры фланцев сосудов и аппаратов

Рис. 1. Фланцы сосудов и аппаратов
высокого давления:
а — кованые приварные;
б — кованые, сопряженные
с многослойной обечайкой
Конструктивное оформление кованых фланцев, сваренных с однослойной или многослойной цилиндрической обечайкой, показано на рис.1. Необходимо соблюдать следующие конструктивные соотношения:
1. Диаметр окружности центров шпилек определяют по формуле (1):
 , (1)
, (1)
где z - число шпилек.
2. Для затворов с плоской стальной прокладкой должно также соблюдаться условие D3 ≥ 1,05 D6 + dр, где D6 — наибольший диаметр выточки под уплотнение.
3. Наружный диаметр фланца D2 ≥ D3 + 2dp.
4. Рекомендуемый угол наклона образующей конической части фланца α ≤ 30°; допустимо 30° < α ≤ 45°.
5. Размеры h3 и h6 находят из следующих условий:
при α ≤ 30°: h3 > Ip + 0,25dp и h6 > 0,7sR;
при 30° < α ≤ 45°: h3 ≥ Ip + 0,75dp и h6>sR.
Значение lp определяют отдельно.
Исполнительная толщина s стенки цилиндрической части фланца, стыкуемой с обечайкой корпуса, должна быть не менее sR: определяемой по формуле
 , (2)
, (2)
где R - внутренний радиус сосуда, p -расчетное внутренне давление, φ(σ) - коэффициент прочности сварных соединений, σ - напряжение, с -суммарная прибавка к расчетной толщине . Также исполнительная толщина s должна быть не менее толщины стыкуемой с фланцем обечайки. При s > sM (рис. 1,б)толщину многослойной обечайки в месте стыка с фланцем следует увеличить до толщины s введением дополнительных слоев на длине  . При s/sM < 1,2 разрешается не вводить дополнительные слои; в этом случае на фланце в месте стыка с многослойной обечайкой выполняют скос.
. При s/sM < 1,2 разрешается не вводить дополнительные слои; в этом случае на фланце в месте стыка с многослойной обечайкой выполняют скос.
↑ В начало
Оценка прочности фланца сосуда или аппарата
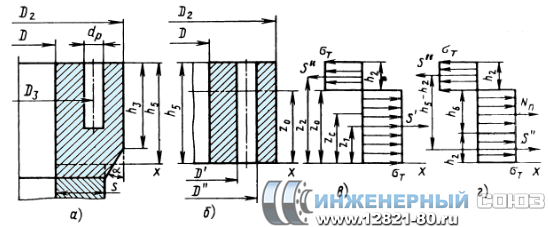
Рис. 2. Расчетные схемы фланцев сосудов и аппаратов:
а - фланец с корпусом сосуда;
б - выделение кольца фланца для расчета;
в - эпюра напряжений при предельном состоянии фланца;
г - схема растягивающих сил Nn и изгибающего момента Mn
при предельном состоянии фланца
↑ В начало
Расчетная схема для оценки прочности фланца
Прочность фланца оценивают по несущей способности. При этом для расчета по перечное сечение фланца с коническим переходом заменяем прямоугольным поперечным сечением (рис. 1,а) высотой h5 = h3 + 0,25 (D2 - D - 2s)/tg α.
При расчёте рассматриваем кольцо фланца, отсеченное от цилиндрической части корпуса, с отверстием под шпильку с диаметром dp на всю высоту фланца h5 (рис. 2,б). Предполагаем, что несущая способность кольца фланца исчерпывается при образовании пластического шарнира в диаметральном сечении фланца под действием изгибающего момента и растягивающей силы. Материал фланца принимаем идеально пластичным. При оценке прочности фланца проверяем, достаточна ли конструктивно выбранная высота фланца h5. В результате расчета определяем условную высоту фланца h6, достаточную для того, чтобы выдержать нагрузку от действующего на фланец внутреннего давления. После этого определяем предельно допускаемый момент, который может выдержать оставшаяся часть фланца. Если этот момент больше момента внешних сил, действующих на фланец, то рассматриваемый фланец удовлетворяет условиям прочности. В противном случае необходимо увеличить высоту h5 фланца и повторить проверку прочности фланца по несущей способности.
↑ В начало
Исследование и расчет предельного напряжения фланцев сосудов и аппаратов
Предельная растягивающая сила
Эпюры напряжений при потере несущей способности фланца приведены на рис. 2, в. Разность равнодействующих растягивающих S' = σTF1 и сжимающих S" = σTF2 напряжений должна быть равна предельной растягивающей силе Nn от давления:
S' - S'' = σT(F1 - F2) = Nn = p⋅0,5Dh5nT, (3)
где F1 и F2 - площади поперечных сечений фланца, находящиеся под действием соответственно растягивающих и сжимающих сил; p - внутреннее давление; nT = 1,5 - коэффициент запаса прочности по пределу текучести.
Расстояние до нейтральной оси z0 определяем из выражения (3), учитывая, что
F1 = 0,5 (D2 - D - 2dp) z0 и F2 = 0,5 (D2 - D - 2dp)(hs - z0);
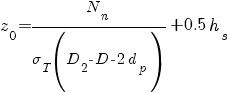
↑ В начало
Предельный момент сечения фланца
Зная предельную растягивающую силу Nn, определяем предельный момент Мn, для рассматриваемого сечения фланца (рис. 2, в)
Mn = S'(zc - z1) + S''(z2 - zc), (4)
где zc - расстояние от оси x до центра тяжести сечения фланца, z1 и z2 - расстояния от оси x до точек приложения равнодействующих S' и S''.
Обозначив b = 0,5 (D2 - D - 2dp ), можно представить формулу (4) в виде (рис. 2,г):
Мn = σTb(h5 - h2)[0,5h5 - 0,5 (hs - h2)] + σTbh2[(hs - 0,5h2 ) - 0,5h5] = σTbh2(h5 - h2) = S''(h5 - h2).
Таким образом, если известна высота h6 сечения фланца (рис. 2, г), на которой фланец переводится в пластическое состояние растягивающей силой Nn то предельный момент
Мn = S''(h5 - h2) = σTbh2(h5 - h2), (5)
где h2=0,5(h5 - h6).
↑ В начало
Высота сечения фланца для тонкостенных цилиндров
Значение h6 можно найти из условий Nn — p = 0,5Dh5nT и Nn = σTbh6. Отсюда
σTbh6 = 0,5pDh5nT , (6)
следовательно, h6 =рDh5nT / (2σTb).
Выражение (6) можно записать следующим образом:
σTb = 0,5 p' D, p' = 2σTb/D, (7)
где р' - давление, при котором материал тонкостенного цилиндра переходит в пластическое состояние.
С другой стороны, из (6) и (7) следует р' = ph5nT / h6, отсюда
h6 = ph5nT/p' . (8)
Таким образом, высоту h6 можно определить по известному расчетному давлению р и давлению, переводящему цилиндр с внутренним параметром D и толщиной стенки b в пластическое состояние.
↑ В начало
Высота сечения фланца для толстостенного цилиндра
Формулы (7) справедливы лишь для тонкостенных цилиндров. Для толстостенных цилиндров предельное давление
p' = σT lnβ, (9)
где β = D2/D - коэффициент толстостенности рассматриваемого цилиндра.
При определении давления р' по формуле (7) ослабление сечения фланца отверстием под крепеж учтено введением b = 0,5 (D2 - D - 2dp ).
↑ В начало
Учет ослабления фланца крепежными отверстими для толстостенного цилиндра
Учтём ослабление фланца шпильками для толстостенного цилиндра. Будем считать, что перемычки между шпильками (болтами) и сами шпильки (болты) не передают кольцевых напряжений, а передают только радиальную нагрузку.
Выделим во фланце три цилиндра (см. рис. 2, б) первый цилиндр с внутренним диаметром D и наружным D' , второй - с диаметрами D' и D'', третий - с диаметрами D" и D2. Пусть второй цилиндр, содержащий z шпилек (болтов) и перемычек, полностью передает радиальную нагрузку и не передает кольцевых напряжений. Обозначим давление на границе первогр и второго цилиндров р1, на границе второго и третьего цилиндров - р2. Тогда первый и третий цилиндры находятся в предельном состоянии, если выполняются соотношения:
(p' - p1) = σT lnβ'; p2 = σT lnβ'', (10)
где β' = D'/D; β'' = D2/D'' ; D' = D3 - dp; D'' = D3 + dp.
Из геометрических соотношений следует, что р1 = p2D'' / D'. Из формул (10):
[ p' - (D''/D')σT lnβ'' ] = σT lnβ'.
Окончательно для цилиндра со шпильками предельное давление
p' = σT [ lnβ' + (D'' / D' )lnβ'' ] . (11)
По этому значению p' определим уточненное значение
h6 = ( p/p' )h5nT. (12)
Предельный момент, как и ранее, найдем из соотношений (5) :
Mn = σT bh2(h5 - h2),
где h2 = 0,5(h5 - h6).
↑ В начало
Окончательные выражения для предельного давления и допускаемого момента
Так как при определении предельного состояния элементов сосудов в отечественных и зарубежных стандартах принято использовать наименьшую из двух величин [σT/nT; σВ/nВ ] , то окончательно выражения для предельного давления и допускаемого момента имеют вид:
p' = σmin [ lnβ' + (D'' / D' )lnβ'' ]; (13)
[M] = σmin bh2(h5 - h2),
где σmin = [ σT/nT; σВ/nВ ].
↑ В начало
Окончательно выражение для высоты сечения фланца
Теперь можно найти окончательное выражение для определения h6:
 . (14)
. (14)
Подставив в выражение для изгибающего момента (13) b = 0,5(D2 - D - 2dp) и h2 = 0,5(h5 - h6), получим допускаемый момент для рассмотренного сечения фланца:
[М] = 0,125 σmin (D2 - D - 2dp) (h52 - h62). (15)
↑ В начало
Условие прочности фланца на изгиб
Условие прочности фланца на изгиб в диаметральном сечении имеет вид
М<2[М], (16)
где M — изгибающий момент относительно диаметрального сечения фланца от действия приложенных нагрузок.
Для определения изгибающего момента М введем следующие обозначения:
- FB - расчетная осевая сила, действующая на шпильки (болты и гайки) при расчётном давлении;
- FP - осевая сила от действия уплотнительного кольца или прокладки;
- FQ1 - осевая сила, действующая на поперечное сечение стенки примыкающего к фланцу цилиндра;
- FQ2 - осевая сила, действующая на участок торца фланца, заключенный между внутренней поверхностью сосуда и средней линией уплотнительной поверхности.
Для определения изгибающего момента рассмотрим половину кольца фланца. Тогда равнодействующие указанных сил составят:
- R1 = 0,5FB;
- R2 = 0,5FP;
- R3 = 0,5FQ1;
- R4 = 0,5FQ2;
расстояния от точек их приложения до диаметрального сечения:
- l1 = D3 / π;
- l2 = DR / π;
- l3 = (D + s) / π;
- l4 = 0,5 (D+DR) / π.
Изгибающий момент:
М = (0,5/π)[FB D3 - FQ1(D+s) - FPDR - FQ20,5(D + DR)]. (17)
↑ В начало
Алгоритм расчета фланцев сосудов и аппаратов по предельному состоянию
Таким образом, расчет фланца по предельному состоянию выполняется в следующем порядке:
- По формуле (17) находится изгибающий момент М относительно диаметрального сечения.
- Определяется расчетная высота фланца h5.
- По формуле (14) рассчитывается высота h6 условного цилиндра, гарантирующая прочность фланца от действия внутреннего давления.
- По формуле (15) определяется допускаемый момент [М].
- Проверяется условие (16) прочности фланца на изгиб в диаметральном сечении. Если условие (16) не выполняется, то необходимо
- увеличить высоту h5 цилиндрической части фланца или его наружный диаметр и повторить расчет.
↑ В начало
Заключение
Точный расчет фланцев сосудов и аппаратов - сложная инженерная задача. В данной статье указан относительно простой аналитический метод приближенного нахождения основных геометрических характеристик фланцев сосудов и аппаратов методом последовательных приближений. Зачастую данного метода хватает для принятия решения о типе и размере необходимого фланца для промышленного аппарата или сосуда.
↑ В начало
Список литературы
- Волошин А.А., Григорьев Г. Т. Расчет и конструирование фланцевых соединений : Справочник.. – Л.: Машиностроение, 1979. – 125 c.
- Канторович З.Б. Основы расчета химических машин и аппаратов.. – М.: Машгиз, 1960. – 743 c.
Получив доступ к данной странице, Вы автоматически принимаете Пользовательское соглашение.