Сферические днища. Фланцевые заглушки сосудов и аппаратов.

Фланцевое соединение сферического днища с корпусом сосуда или аппарата. В каком-то приближении днища - это заглушки (глухие фланцы) сосудов и аппаратов.
Сосуды, аппараты, корпуса высокого давления зачастую выполняются со съёмными сферическими днищами фланцевого крепления. Фланцевые соединения сферических днищ и цилиндрических оболочек имеют широкое применение в энергетике, химической, нефтехимической промышленности и в других отраслях техники.
Дата публикации: 13 апреля 2011
Сфера применения фланцевых днищ (заглушек) сосудов и аппаратов
Рассмотрим фланцевые соединения сферических днищ и цилиндрических оболочек. Такие соединения имеют широкое применение в энергомашиностроении, в химическом машиностроении и в других отраслях техники. В каком-то приближении днища – это заглушки (глухие фланцы) сосудов и аппаратов.
Конструкция фланцевого соединения сферических днищ, крепеж болтами
Часто рассматриваемые фланцевые соединения выполняются по типу, изображенному на рис. 1, а, то есть днище с корпусом 1 соединяется с помощью болтов, заворачиваемых в отверстие фланца цилиндра.
Крепление с утопленными болтами
Цилиндр 1 у фланца 2 несколько утолщается снаружи для обеспечения равнопрочности ослабленного болтовыми отверстиями и неослабленного сечений. Нередко выполняются соединения с утопленными головками болтов. В общем случае цилиндрическое сечение, проходящее через оси болтовых отверстий, не совпадает со срединной поверхностью цилиндра. При таком выполнении конструкции можно достигнуть отсутствия изгиба в зоне перехода цилиндрической оболочки во фланец 1 (рис.1, а), подбирая определенным образом радиус центров болтовых отверстий и коэффициентов затяга крепежа. На рис.1, а даны обозначения конструкции, а на рис1, б показаны искомые и заданные нагрузки.
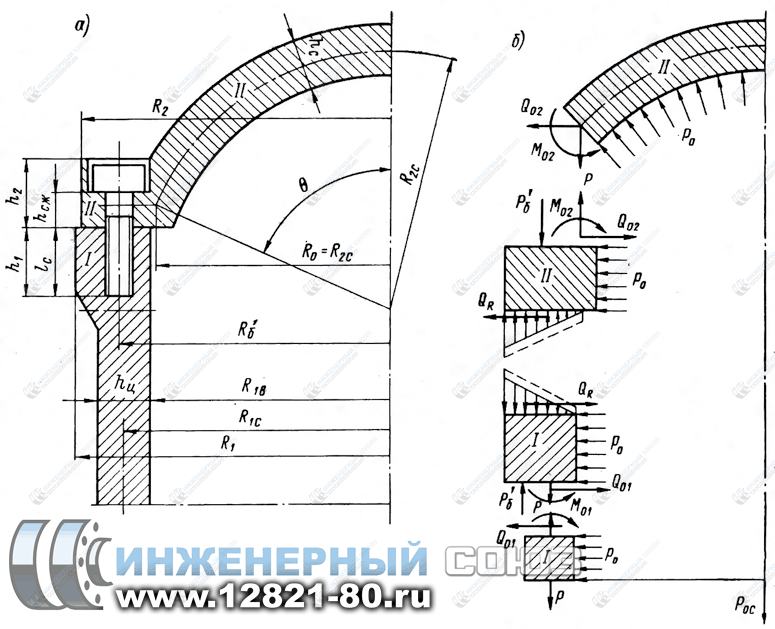
Рис. 1. Конструктивная и расчетные схемы фланцевого соединения корпуса
сосуда или аппарата со сферическим днищем
Конструкция типа "болты-гайки"
Конструкция соединения с утопленными болтами, вворачиваемыми в отверстия цилиндра, позволяет значительно сократить наружные размеры фланцев цилиндра и днища по сравнению с конструкцией соединения с помощью болтов и гаек. Однако в этой конструкции существенно ослабляются фланцы цилиндра и днища за счет значительных выточек под головки болта и резьбы в цилиндре. В ней, как правило, податливость соединения с креплением типа "болты-гайки" за счет значительного уменьшения размеров сечений конусов давления. В результате этого коэффициент основной нагрузки болтов соединения такого типа ( рис.1, а) больше, чем в сопоставляемой конструкции.
Но в конструкции соединения, выполненного, как показано на рис.1, а, легче уменьшить напряжение изгиба во всех расчетных сечениях и обеспечить требуемую плотность соединения.
Расчет фланцевых соединений сосудов и аппаратов со сферическими днищами
Ниже даны два метода расчета таких фланцевых соединений. В первом дается полная система уравнений, включающая полные условия сопряжения элементов фланцевого соединения. Решение этой системы позволит выполнять полный расчет конструкции.
Во втором методе при использовании упрощенных условий сопряжения даются конечные формулы.
Решение полной системы уравнений на соединение глухого сферического фланца с сосудом или аппаратом
Полная система уравнений имеет следующий вид:
Δс = -α11Q02√ sinΘo α12M02 + α13Po; (1)
ϑс = α21Q02 – α22M02– (α21PoRo/ 2) ctgΘ0; (2)
ω2 = λ2QQ02 ¯ λ2pP0¯ h2*φ2 ; (3)
ω2' = λ2QQ02 ¯ λ2pPo +h'2* φ2 ; (4)
φ2 = λ21Poc ¯ λ22M02 ¯ λ23Q02; (5)
ω1 = λ1QQ01 ¯ λ1ppo¯ h1*φ1 ; (6)
ω1 = λ1QQ01 ¯ λ1pp0+ h'1*φ1 ; (7)
φ1 = λ'21Poc ¯ λ'22M01 ¯ λ'23Q01; (8)
Δц = αц11Q01 + αц12M01 + αц13po; (9)
φц = αц11Q01 + αц22M01 + αц23po; (10)
φ'1 + φ'2 = ϑc + φц; (11)
Δс = ω1; (12)
ϑc = φ1; (13)
Δц = ω2; (14)
ϑц = φ2; (15)
φ1 + φ2 = ϑc + φц; (16)
ω'1 = – ω'2; (17)
где обозначено
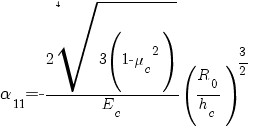

![alpha_{22} = - {4 delim{[}{3(1-{mu_c}^{2})}{]}^{3/4}}/{E_c {h_c}^2 } sqrt{{R_0}/{h_c}} alpha_{22} = - {4 delim{[}{3(1-{mu_c}^{2})}{]}^{3/4}}/{E_c {h_c}^2 } sqrt{{R_0}/{h_c}}](/images/tech/119/math_968_decf1a5d35afee5e0b52bd9a3afeaacd.png)
![alpha_{13} = {R_0}/{E_c}delim{[}{ {1 - 0.5 mu_c }/{sin Theta_0} {R_0}/{h_c} - root{4}{3(1-{mu_c}^{2})} sqrt{sin Theta_0} ctg Theta_0 ({R_0}/{h_c})^{3/2} }{]} alpha_{13} = {R_0}/{E_c}delim{[}{ {1 - 0.5 mu_c }/{sin Theta_0} {R_0}/{h_c} - root{4}{3(1-{mu_c}^{2})} sqrt{sin Theta_0} ctg Theta_0 ({R_0}/{h_c})^{3/2} }{]}](/images/tech/119/math_941.5_f34b3c21d2d0083411b9a3cc8dd62e0a.png)
![lambda_{i1} = { R_{ic} delim{[}{ k_i - 1 + m_i - ({b_1}/{R_{ic}} + f_c h prime_{i*} ) (kappa + chi - psi - 1) }{]} }/{ 2 pi overline{E_i} } lambda_{i1} = { R_{ic} delim{[}{ k_i - 1 + m_i - ({b_1}/{R_{ic}} + f_c h prime_{i*} ) (kappa + chi - psi - 1) }{]} }/{ 2 pi overline{E_i} }](/images/tech/119/math_974_683780d92d9fe3e01c26ac9149b59adc.png)
λi2 = Ric/Ei;
λi3 = λi2hi;
Ei = EiJix/(1-µ2i) + E6d26na1b1/ (8Jib);
λ1Q = (1-µ2i) / Eihi ln kiB; ki = Rб / Ric;
λip = (1-µ2i) / Ei ln kin; ki = Ri/ Rib;
αц11 = λ'0Q = (2ß3ц Dц)-1;
αц12 = αц21 = (2ß2цDц)-1;
αц13 = λ'op = (4ß4цDц)-1;
αц21 =αц12;
αц22 = λ1φom = (ßцDц);
αц23 = λ1φop = 0.
Первые два соотношения (1) и (2) предыдущей системы, определяющие перемещения точек края сферической оболочки, загруженной, как показано на рис.1,б, приведены в работе [3]. Направление радиального перемещения от центра принято в выражении (1) за положительное направление. Угол поворота считается положительным, если он увеличивает кривизну оболочки.
Соотношения (3) — (8) даны ранее. В них направление перемещений точек фланцев к оси фланцев считается положительным.
Углы поворота сечений фланцев считаются положительными, если при увеличении абсолютная величина контактных напряжений уменьшается со стороны приложения сил P (рис.1, б). Поворот сечения фланца I по часовой стрелки, а фланца II - против часовой стрелки соответствуют положительным углам.
Формулы (9) И (10) известны [4]. Они определяют перемещения точек и краевого сечения цилиндрической оболочки I.Эти формулы можем получить из приближенного решения дифференциального уравнения краевой задачи для конической оболочки переменной жесткости, положив tgα = 0. Направление радиального перемещения от центра цилиндрической оболочки принято положительным. Угол поворота сечения считается положительным, если поворот сопровождается растяжением наружной образующей цилиндрической оболочки. Остальные уравнения системы ясны из предыдущего изложения.
Предыдущая система содержит 18 неизвестных. Из них две неизвестные величины - коэффициент затяга κ и ширина нераскрытия X01 - взаимосвязаны соотношениями.
Если задаваться, как прежде, для частично раскрывающихся фланцевых соединений величиной X01 то остаются 17 неизвестных, которые определяются из этой системы.
Численное решение предыдущей системы нелинейных алгебраических уравнений на ЭВМ не представляет труда.
Упрощение системы уравнений на фланцевое соединение
Расчеты показывают, что часто эта система может быть упрощена путем введения дополнительных допущений в исходную задачу. В результате этого можно получить удобные для практического использования формулы.
Для этой цели, прежде всего, откажемся отвыполнения условия совместимости радиальных перемещений точек стыка и приравняем нулю касательные силы по плоскости разъема, т.е. примем QR = 0. В результате этого из системы могут быть опущены соотношения (4), (7) и (17).
Поставим ослабленные сопряжения оболочек с фланцами, приравняв нулю радиальные перемещения точек сопряжений оболочек с фланцами. Из этих условий получим, используя (1) и (9), следующие соотношения между перерезывающими силами и моментами:
Q01 = ßцM01 - p/ (2ßц); (18)
Q02 =α12 / (α11√sinΘo M02) + α13 / (α11Rop); (19)
Преобразуя предыдущую систему в соответствии с отмеченными допущениями, получим:
ϑс = αoM02 + αopσ; (20)
φ2 = λ'21Poc ¯ λ'22M02 ¯ λ'23Q02; (21)
φ1 = λ21Poc ¯ λ22M01 ¯ λ23Q01; (22)
ϑс = M01/(ßцDц) + p/(4ß3цDц) ; (23)
φ1 + φ2 = Poc (λфκ - λбκ) / X01; (24)
ϑс = φ2; (25)
ϑn = φ1 ; (26)
φ'1 + φ'2 =φ1 + φ2 = ϑс + ϑц; (27)
Последняя упрощенная система из восьми уравнений содержит следующие восемь неизвестных: M01, M02, ϑс , ϑц, φ1, φ2, φ'1 + φ'2, и κ. Эта система является замкнутой, если, как и прежде, задаваться X01.
Разрешая систему относительно искомых, отнесенных к единице длины, моментов и коэффициента затяга, получим:
M01 = Poc/2π { k1 - 1 - b1/R1c (κ +χ-ψ - 1) +pk/A1; (28)
M02 = Poc/2π { k2 - 1 - b1/R2c (κ +χ-ψ - 1) +pαp/α; (29)
κ = 1+ φ -x + λ1ф/(1+ λ1фb1){R1 -1 +m1 +α1(R2 - 1+ m2)+k p/Poc}, (30)
где обозначено
A1 = 1 + ßцh1+ (1-µ21)/(4ßцR1цhцl'1b) ⋅ (2h31l1b ln k +3d2bna1b1);
k = πh/ (ßцPoc); h = h1+ E1/ (2ß2цR1cDц);
αp = α13/α11Roh - E1- (α21ctgΘo +α12α13/α11)Ro;
α* = 1+α12h1* / (α11√sinΘ0)+E1 [ -α22 + α122 / (α11√sinΘ0);
λ*1ф = X01 / (2π λфβцDцE1)
b1* = b1/R1c + a1* b1/R0
a1* = E1/E2⋅R0/R1c;
m1 = Py/Poc⋅Ry/R0 (Rб/Ry - 1); m2 = Py/Poc⋅Ry/R1 (Rб/Ry - 1);
k* = 2παp - 2πk/α1* + (α13 + 1/(4ß3цDц))2πα*α1* / α0 ;
α0p = (-0.5α11 ctgΘo + α12α13/α11)R0;
Dц = Ец h3ц /10.92.
Последние коэффициенты записаны при µ = 0.3.
Определив по предыдущим формулам значения коэффициента затяга и внутренних усилий, действующих в сечениях сопряжений элементов и соответствующих заданной плоскости, можно подсчитать напряжения в оболочке, пластине, во фланцах и в болтах.
Заключение
Таким образом, расчет фланцевых соединений днищ сосудов и аппаратов может производиться численными методами на ЭВМ. В последнее время в связи с развитием систем автоматизированного проектирования многие расчеты деталей трубопроводов проводятся с использованием электронной вычислительной техники.
Список литературы
- Волошин А. А. Расчет фланцевых соединений трубопроводов и сосудов.. – Л. : Судпромгиз, 1959. – 365 c.
- Бугов А. У. Инженерный методы расчета симметричных кольцевых фланцевых соединений гидротурбин // Энергомашиностроение, 1970, №10... – с. 5-7.
- Новожилов В. В. Теория тонких оболочек.. – Л. : Судпромгиз, 1962. – 430 c.
- Тимошенко С. П., Войновский-Кригер С. Пластинки и оболочки.. – М. : Физматгиз, 1963. – 345 c.
Получив доступ к данной странице, Вы автоматически принимаете Пользовательское соглашение.