Краевая задача на воротниковые фланцы

Имя воротниковому фланцу даёт воротник - коническая оболочка, которой фланец приваривается встык к трубе.
Воротниковые фланцы отличаются от плоских фланцев так называемым "воротником", от которого и получили своё неофициальное название. Воротник фланца стального приварного встык имеет форму конической оболочки. Определим дифференциальное уравнение для постановки краевой задачи.
Дата публикации: 6 апреля 2011
Применение воротниковых фланцев
В тонкостенных оболочках, имеющих фланцевые соединения, области переходов от фланцев выполняются в виде конических оболочек, толщина которых изменяется по линейному закону. Воротниковые фланцы — фланцы, снабженные такими коническими оболочками.
Определение напряжений изгиба в воротнике фланца
Для определения изгибных напряжений в сечениях переходных конических оболочек (в воротнике фланца) I и II (рис. 1, б в статье "Задачи расчета фланцевых соединений валов гидротурбин") должны быть найдены краевые усилия Qoi и Moi ( i = 1,2) и установлен закон изменения этих усилий в сечениях оболочек. Эта задача связана с необходимостью вывода и интегрирования разрешающего дифференциального уравнения краевой задачи.
Эта задача решается путем численного интегрирования исходного дифференциального уравнения краевой задачи, методом конечных разностей, методом двух аппроксимаций и др. Общим недостатком этих методов является их сложность и невозможность получить замкнутые соотношения между перемещениями срединной поверхности оболочки и действующими усилиями в общем виде. Ниже выводится приближенное дифференциальное уравнение краевой задачи для оболочек рассматриваемого типа и дается его асимптотическое интегрирование.
Вывод дифференциального уравнения на коническую оболочку фланца стального приварного встык
Для вывода уравнения на коническую оболочку приварного встык стального фланца, следуя И.Я. Штаерману рассматривается элемент оболочки, выведенный двумя близко расположенными диаметральными сечениями, как балка переменной жесткости на упругом основании (рис. 1, а -в).
Геометрическое выделение бесконечно малого элемента воротникового фланца
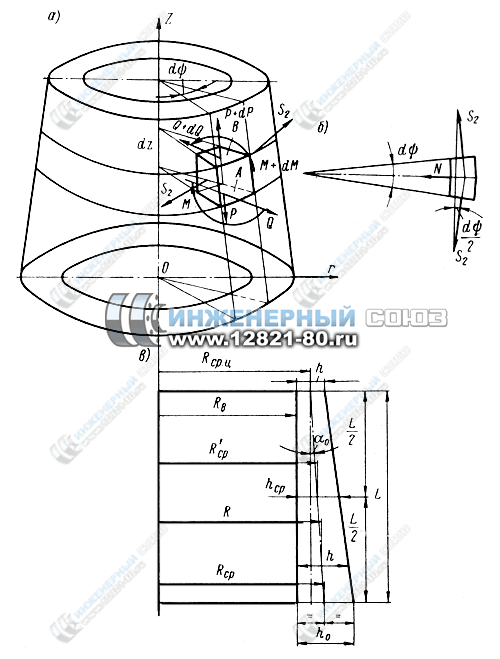
Рис. 1. К расчету конической оболочки
Для определения реакции упругого основания выделяется элементарное кольцо высотой dz (рис.1, а), двумя поперечными сечениями. Под действием нагрузок все точки оси этого кольца перемещаются в радиальном направлении на величину ω.
Относительное удлинение осевого волокна и кольцевое усилие, возникающее в нем, равны:
Ez = ω / R; (1)
S2 = (ω / R) Eh ds, (2)
где R = Rcp — z tgα0 – радиус среднего кольцевого волокна (рис.1, в); ds – длина образующей усеченного конуса высотой dz.
Выделим двумя диаметральными сечениями, образующими угол dφ, элемент кольца (рис. 1, а и б).
Силы, действующие на элементарный элемент конической оболочки воротникового фланца
На выделенный элемент воротникового фланца будут действовать следующие силы и моменты: на грань А (рис.1, а) действует момент MRdφ, перерезывающая и осевая силы QRdφ и PRdφ; на грань В действуют соответственно (M + dM) Rdφ, (Q +dQ) Rdφ и (P +dP) Rdφ, по боковым граням действуют S2 и N.
Проекция сил S2 на направление N (рис.1, б) равна
N = 2 S2sindφ/2 = ω/R Ehdsdφ, (3)
где h = h0 — 2 tgα0 – толщина оболочки в данном сечении.
Сумма моментов относительно оси, касательной к параллельному кругу и проходящей через центр тяжести грани В, равна
(M +dM) Rdφ - MRdφ - QRdzdφ - (ω/R) Eh (dz)2/2 - PRtgα0 dz dφ = 0.
Отбрасывая величины второго порядка малости и разделив все слагаемые на Rdzdφ, получим из последнего уравнения
Q = dM / dz — P tg α0. (4)
Сумма проекций всех сил, действующих на выделенный элемент, на горизонтальную ось дает
(Q + dQ) R dφ — Q R dφ — N = 0.
Из последнего уравнения можно получить
N = (dQ/dz) R dz dφ. (5)
Дифференцируя (4) по z, используя (3) и (5), получим
d2M / dz2 = (ωEh / R3) (ds / dz) + (dp / dz) tgα0 (6)
В дифференциальное уравнение (6) входят две неизвестные функции: M и ω. Для исключения одной из них следует составить еще одно уравнение.
Воспользуемся известным соотношением
M / (EJ) = dϑ / ds, (7)
где ϑ — изменение угла α0 вследствие деформации осевой линии балки-полоски, выделяемой из оболочки; M — изгибающий момент в сечении балки-полоски.
Воспользуемся соотношением
ϑ = dω / dz.
Дифференцируя последнее выражение по s, получим
dϑ / ds = d2ω / (dz ds). (8)
Подставляя последнее выражение в (7) и заменяя жесткость на изгиб балки цилиндрической жесткостью оболочки, получим
D (d2ω / dz2) (dz / ds) + M = 0, (9)
где
dz / ds = cos α0.
При выводе последнего уравнения принималось:
EJ = DR dφ;
Mб = MR dφ,
где D - цилиндрическая жесткость оболочки в данном сечении, равная
D = (E0h3) / {12(1 -µ02)};
E0 и µ0 — модуль упругости и коэффициент Пуассона материала оболочки; M – изгибающий момент относительно средней окружности поперечного сечения оболочки.
Дважды дифференцируя выражение (9) по z, получим
( d2(D d2ω/dz2) / dz2 ) cos α0 + d2M / dz2 = 0. (10)
При дифференцировании (10) следует помнить, что жесткость оболочки является переменной величиной, так как толщина оболочки (рис.1) изменяется по линейному закону, уменьшаясь с увеличением z. Из двух дифференциальных уравнений (6) и (10) можно исключить неизвестную функцию M и получить уравнение относительно функции ω.
Прежде чем проделать эту операцию, преобразуя последнее слагаемое в (6), исходя из того, что
P = Poc/ {2π ( R0 - ztgα0)}.
Дифференцируя последнее выражение по z, получим
dP / dz = - Poc tgα0/ 2π ( R0 -ztgα0)2. (11)
Выполняя операции дифференцирования выражения (10) и используя формулы (6) и (11), получим из (10) после всех преобразований следующее дифференциальное уравнение задачи:
d4ω / dz4 + (2/ (Dcosα0)) ⋅ (dD/dz) ⋅ d3ω/dz3 + 1/(D cosα0) ⋅ d2D/dz2 d2ω/dz2 + (Eh)/(DR cos2α0) ⋅ ω + (Poc tg2α0)/(2πR2D cos2α0) = 0, (12)
где
2/(D cos α0) dD/dz = - 12 tgα0 / (h0 - 2z tgα0); (13)
1/D d2D/dz2 = 24 tg2 α0/(h0 -2ztgα0)2. (14)
Заключение
Важнейшим этапом решения задачи по расчету воротникового фланца является вывод дифференциального уравнения конической оболочки (воротника), ведь именно эта деталь по многим параметрам выгодно отличает фланцы воротниковые от плоских фланцев.
Список литературы
- Тимошенко С. П. Сопротивление материалов.. – М. : Гостехиздат, 1943. – 345 c. Т. 2.
- Волошин А. А. Расчет фланцевых соединений трубопроводов и сосудов.. – Л. : Судпромгиз, 1959. – 365 c.
- Макаренков А. Г. Исследование напряженного состояния фланцевого соединения с учетом физической нелинейности материала // «Прикладная механика». Отд. математики, механики и кибернетики. Изд-во АН УССР, 1970, т. VI, вып. 2... – с. 45—48.
Получив доступ к данной странице, Вы автоматически принимаете Пользовательское соглашение.