Кинематика деформации несимметричных фланцевых соединений второго рода
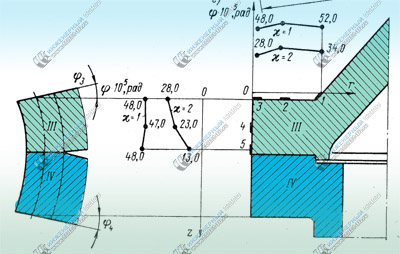
Деформация изгиба в болтах и в эффективных объемах фланцев за счет поворота торцовых образующих фланцев. Кольцевые напряжения в объёме стальных фланцев.
Несимметричные фланцевые соединения второго рода образованы двумя неодинаковыми наружными фланцами, соединенными с оболочками различного типа. Применяются фланцы таких типов в соединениях корпусов реакторов, резервуаров, сосудов, аппаратов, рабочих колес гидротурбин с днищами и крышками.
Дата публикации: 31 марта 2011
Условия осесимметричности деформации фланцевого соединения
При рассмотрении кинематики деформации фланцевого соединения принималось, что деформированное состояние является осесимметричным. Это предположение может быть принято за рабочую гипотезу, если:
- шаг расположения болтов t1 (рис. 1, а) и высоты фланцев h3 и h4 (рис. 1, б), таковы, что сечения конусов сжатия, определяемые уголом α (рис. 1), перекрываются в цилиндрическом сечении, проходящем через центры болтовых соединений,
- а в меридиональных сечениях, проходящих через оси болтов (рис.1, б), максимальные диаметры конусов сжатия (рис.1, г ) равны или больше радиальной ширины плотного прилегания фланцевого соединения t (рис. 1).
Цикличная симметричность при удалении болтов друг от друга
При достаточно большом удалении друг от друга центров болтовых отверстий, когда конусы сжатия не перекрываются (рис.1, а), деформированное состояние фланцевого соединения от затяга болтов будет иметь циклически симметричный характер, причем затяг болтов может вызвать образование зазоров в средней части между болтовыми отверстиями на участках а (рис. 1, а) В этом случае результаты расчетов, основанных на предположении об оссесимметричном деформированном состоянии, могут дать большую погрешность.
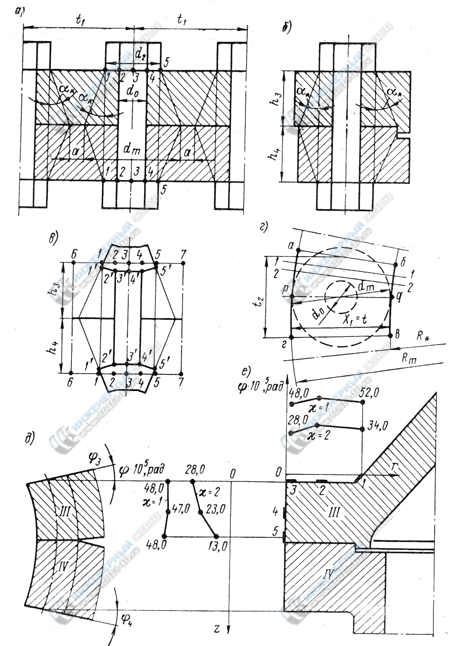
Рис.1. Схема деформации нессиметричного фланцевого
соединения второго рода
Сопоставляя результаты расчетов осевых податливостей, полученным по известным формулам Биргера и Иосилевича и по формулам, базирующимся на представлении об осесимметричной деформации фланцевого соединения, можно заключить, что предположение об осевой симметрии деформированного сотояния может дать погрешность, превосходящую 15 %, если t1 и t > d1+ h1 tg α.
Углы поворота наружной поверхности фланцев в области болтовых отверстий и между ними
Для оценки отличия реального деформированного состояния при осевом нагружении во фланцевом соединении от осесимметричного проводились замеры углов поворота на наружной поверхности фланцев сосудов и резервуаров в меридиональных сечениях, проходящих по осям болтов и посредине между болтовыми отверстиями в точках 1-5 (рис. 1, е), при числе болтов равном 20, 12, и 8. Болты были установлены по окружности радиусом 96 мм. Диаметры стержня и головки болтов были равны db =15 мм, и dr = 21 мм. В таблице приведены значения замеренных углов поворота у края торца фланцев по оси болтов и между осями в зависимости от отношения шага расстановки к наружному диаметру головки болтов (t1/dr).
| № модели | n, шт. | κ | t1, мм | t1/dr | Угол поворота сечения φ⋅105, рад | 100%⋅( (7)—(6) )/(6) | |
| по оси болтов | между осями | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 20 | 1,40 | 28,6 | 1,36 | — | 48,4 | — |
| 2 | 12 | 1,07 | 47,6 | 2,27 | 63,4 | 68,9 | 8,80 |
| 3 | 8 | 0,72 | 71,5 | 3,40 | 65,0 | 76,2 | 17,5 |
Из этой таблицы видно, что углы поворота, замеренные в точках, расположенных на расстоянии 1 см от наружного края фланца в меридиональных сечениях, проведенных по оси болтов и между осями болтов, различаются несущественно. Даже при весьма редко м расположении болтов, когда t1/dr = 3,4, отношение угла поворота (в %), замеренного между осями болтов, к углу, замеренному в точке, расположенной по оси болтов равно 17,5. Это отношение равно 8,80 при t1/dr = 2,27.
Замеры на трубчатой части и в переходной зоне от оболочек к фланцам углов поворота и радиальных перемещений в сравнимых точках меридиональных сечений моделей №2 и 3, проведенных через оси болтов или шпилек и посредине между осями , показали, что заметной разницы в перемещениях точек этих сечений не наблюдается.
Условие неразрывности осевых деформаций фланцев
Допущения для деформаций фланцевых соединений
На основании изложенного можно сформулировать следующие допущения.
Затяг болтов фланцевого соединения вызывает интенсивную деформацию части объемов фланцев ("эффективных объемов"), непосредственно прилегающих к болтовым отверстиям на (рис. 1.а, б и в). На рис. 1, в схематично схематично показаны положения точек 1-5 до деформации и после деформации 1'-5'.Точки 6-6 и 7-7, расположенные в средней части шага t1 не перемещаются, если конуса сжатия не перекрываются.
Осевая сила, приложенная равномерно по центрам тяжести болтов затянутого фланцевого соединения, вызывает равномерную осевую деформацию болтов и эффективных объемов.
Деформации изгиба в болтах и фланцах
Моменты, закручивающие меридиональные сечения фланцев, вызывают деформацию изгиба в болтах и в эффективных объемах фланцев за счет поворота торцовых образующих фланцев III и IV на углы φ3 и φ4 (рис. 1, д) и кольцевые напряжения во всем объеме фланцев.
В результате деформации, вызванной внешними силами, возникает осесимметричное деформированно-напряженное состояние в зоне сопряжения фланцев с оболочками и осесимметричное перемещение наружных контуров фланцев, если выполняется условие t1/dr ≤ 2,5.
Расчетный элемент выделяется из участка абвг плотного прилегания фланцевых соединений (рис.1, г) двумя сечениями 1-1 и 2-2, проведенными на расстоянии 1 см на участке плотного прилегания фланцев. Принимается, что кинематика деформации этого расчетного элемента подобна кинематике деформации расчетного элемента, описанной выше. Последнее предположение замерами углов поворота в точках 1-5 (рис.1, е) меридионального сечения стальных моделей нессиметричных фланцевых соединений второго рода при двух-трех значениях коэффициента затяга. Пределы применимости и достоверность этого допущения те же, что и для несимметричных фланцевых соединений первого рода. Данные замеров по одной модели приводятся на рис.1, е, д.
Допущения на стыковые сечения фланцевого соединения
Далее принимается, что стыковые сечения эффективных объемов имеют форму части кольцевой площади абвг на (рис.1, г) с площадями, равновеликими площадям кольцевых сечений с наружными и внутренними диаметрами dm и d0.
Кинематические допущения
В связи с этим принимаются все основные кинематические допущения. Предположим далее, 1) что для рассчета относительной деформации кольцевых волокон фланца можно использовать выражение
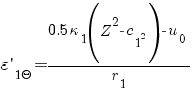 ,
,
где r1 – радиус рассматриваемого кругового волокна фланца, который может изменяться от наружного Rm до внутреннего Rx радиусов площади прилегания фланцев;
u0 – радиальные перемещения точек сечения фланца.
Также предположим, что 2) осевые напряжения будут действовать только по сечениям эффективных объёмов фланцев.
Условие неразрывности осевых деформаций фланца
Для частично раскрывающихся фланцевых соединений может быть получено выражение:
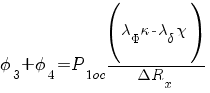 , (1)
, (1)
где
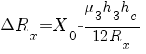 .
.
Здесь
hc = h3c + h4c;
h3c и h4c – высоты фланцев III и IV, сжимаемых при затяге фланцевого крепежа; X0 – длина отрезка отсчитываемого от нераскрытого участка расчетного элемента до точки, в которой контактные напряжения обращаются в нуль (X1 характеризует радиальную ширину нераскрытия фланцев), λФ и χ – податливость фланцевого соединения и коэффициент основной нагрузки, опредляемые, исходя из представления об эффективных объемах.
Уравнение (1) является условием неразрывности осевых деформаций в пределах эффективных объемов, записанным в перемещениях.
Заключение
Для решения задачи сопряжения фланца IV с оболочкой V также могут быть получены соотношения между перемещениями широкого края усеченной пологой конической оболочки и усилиями, действующими на оболочку.
Список литературы
- Макаренков А. Г. Исследование напряженного состояния фланцевого соединения с учетом физической нелинейности материала // «Прикладная механика». Отд. математики, механики и кибернетики. Изд-во АН УССР, 1970, т. VI, вып. 2... – с. 45—48.
- Бугов А. У. Еще раз о расчете напряженного состояния симметричных кольцевых фланцевых соединений валов гидротурбин // «Энергомашиностроение», 1966, № 7... – с. 5-7 c.
- Расчет на прочность деталей гидротурбин / А. Я. Аронсон, А. У Бугов, В. М. Малышев и др... – М.—Л. : Машиностроение, 1965. – 392 c.
Получив доступ к данной странице, Вы автоматически принимаете Пользовательское соглашение.