Расчет несимметричных соединений фланцев третьего рода
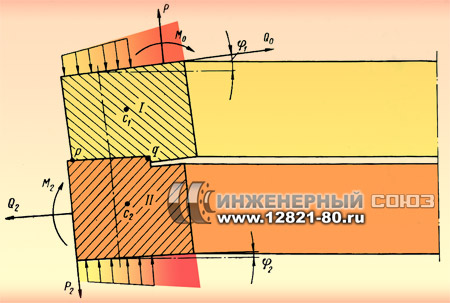
Расчетная схема колец фланцев в случае, когда внешние нагрузки не вызывают раскрытия по всей ширине кольца первоначального прилегания фланцев.
Несимметричные фланцевые соединения третьего рода, используемые в большинстве конструктивных выполнений крышек рабочих колес гидротурбин, также соединяются крепежом через соответственные болтовые отверстия.
Для решения задачи сопряжения нужно составить выражения для перемещений всех характерных точек фланцев и оболочек.
Дата публикации: 5 апреля 2011
Модель деформации фланцевого соединения третьего рода
Продолжим рассуждения о деформации фланцевых соединений третьего рода.
Схема деформированного состояния расчетного элемента стальных фланцев, соответствующая случаю φ1>φ2, представлена на рис.1, а,б,в.
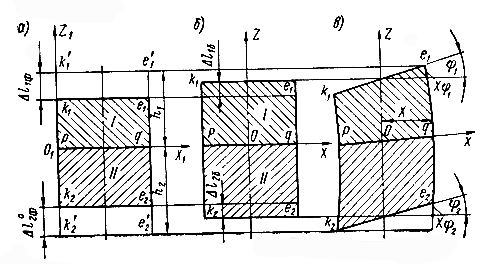
Рис.1 Схема деформации расчетного элемента
Изгибная деформация осевого волокна e1 - e2 (рис.1, в) фланцев, соединённых болтами, в данном случае будет
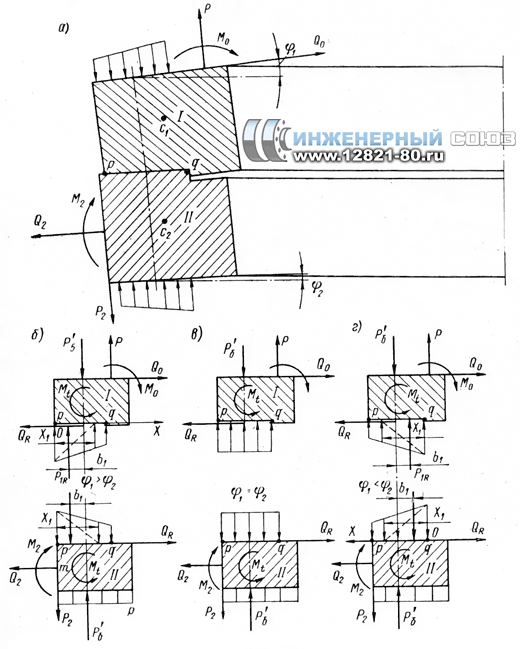
Рис. 2. Расчетная схема несимметричного фланцевого соединения
третьего рода
Δli = X (φ1 — φ2). (1)
Изгибная деформация осевых волокон в случаях фланцевых соединений первого и второго родов определяется как произведение абциссы точки, в которой разыскивается напряжение, на сумму углов. Изменившееся выражение для осевых изгибных деформаций фланцев внесет соответствующие изменения формул. В случае, если φ1< φ2 (рис. 2, г), следует изменить направление оси OX1 и поменять местами углы поворота в формуле (1). В остальном допущения , сформулированные применительно к кинематике деформации несимметричного фланцевого соединения первого рода, считаются справедливыми и для рассматриваемого фланцевого соединения.
Перемещение точек фланцев и оболочек
Для решения задачи сопряжения нужно составить выражения для перемещений всех характерных точек фланцев (аналог фланцев плоских) и оболочек (аналог воротников фланцев приварных встык). Однако составить выражения для двух углов поворота сечений фланцев I и II, справедливые вообще для несимметричных фланцевых соединений третьего рода, невозможно, поскольку заведомо неизвестен характер эпюры нормальных напряжений вдоль p — q (рис. 2),а следовательно, неизвестен знак реактивного момента от P1R.
Случай противоположности реактивного и внешнего моментов, действующих на элемент стального фланца
Рассмотрим сначала случай, когда φ1>φ2 , характерный для большинства конструктивных выполнений крышек рабочих колес гидротурбин и других деталей трубопроводов с фланцевыми соединениями рассматриваемого типа. Для этого случая знак реактивного момента противоположен знаку внешнего момента Mt , действующего на элемент фланца I (рис. 2,б), и направлен в ту же сторону, что и внешний момент для элемента фланца II.
Если определять QR в данном случае выражение для радиального и углового перемещений точек и сечений сопряжения фланца I с оболочкой сохраняются. Как следствие этого, сохраняются выражения для усилий и моментов взаимодействия воротникового фланца I с оболочкой, полученные при удовлетворении полных условий сопряжений фланца и оболочки. Выражения для радиальных перемещений точек фланцев, расположенных на отрезке p — q, сохранятся.
Радиальное перемещение точки m (рис. 2, б) и угол поворота сечения фланца примут вид:
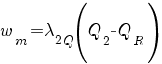 ; (2)
; (2)
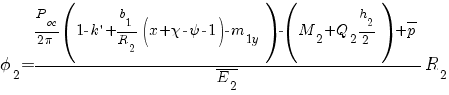 ; (3)
; (3)
где
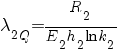 ;
; 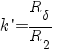 ;
;
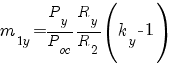 ;
; 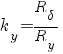 ;
;
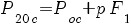 ;
; 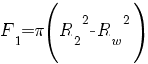 ;
;
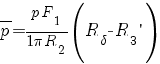 ;
; 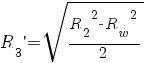 ;
;
Rw – радиус штока механизма поворота лопастей рабочего колеса.
Коническая оболочка - аналогия с воротниковыми фланцами
Выражения для радиального перемещения точки m, относя ее к конической оболочке (коническая оболочка может быть введена по аналогии с воротниковыми фланцами), и угла поворота сечения оболочки, примыкающей к фланцу II, можно получить в виде некоторых уравнений, поменяв в них знак перед моментом на обратный и поменяв индексы перерезывающей силы, изгибающего момента и осевой силы в соответствии с обозначениями на рис. 2, б. Зависимость между суммарным уголом разворота наружных торцов фланцев, податливостью фланцев и болтов, коэффициента затяга и другими параметрами фланцевого соединения получим для случая частичного раскрытия в виде формулы:
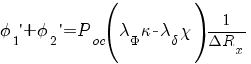 , (4)
, (4)
где
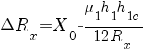 ;
;
h1c – суммарная сжимаемая высота фланцев I и II.
Перерезывающее усилие и изгибающий момент, действующие на фланцы
Считая X1 заданным, из этой системы можно получить выражения для всех искомых величин. Выполнив условие совместимости деформации фланца II и конической оболочки, примыкающей к нему, получим следующие выражения для перерезывающего усилия и изгибающего момента Q2 и M2, действующих на фланцы:
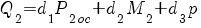 ; (5)
; (5)
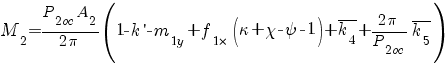 , (6)
, (6)
где
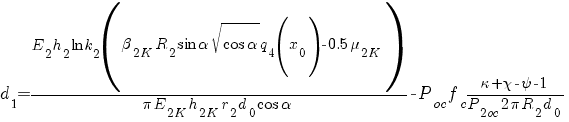 ;
;
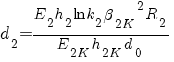 ;
;
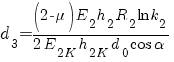
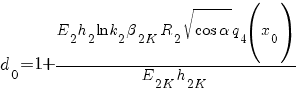
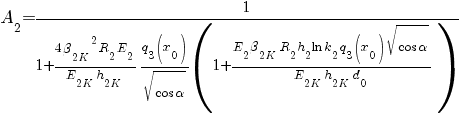 ;
;
![f_{1*} = {P_{oc}}/{P_{2oc}} ( {b_1}/R_2 - {f_c h_2}/{2 R_2}[ 1 - {4 {beta_{2K}}^2 {R_2}^2 E_2 q_3 (x_0) }/{E_{2K} h_{2K} R_2 h_2 d_0 } ] ) f_{1*} = {P_{oc}}/{P_{2oc}} ( {b_1}/R_2 - {f_c h_2}/{2 R_2}[ 1 - {4 {beta_{2K}}^2 {R_2}^2 E_2 q_3 (x_0) }/{E_{2K} h_{2K} R_2 h_2 d_0 } ] )](/images/tech/114/math_926.5_bf59fdf78fca815a8145103ba9c460ed.png) ;
;
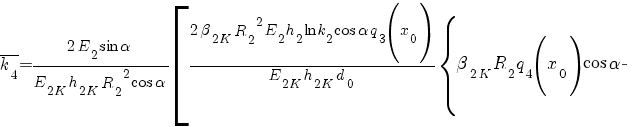
![delim{}{ delim{} {- {0.5 mu_{2K}}/{sin alpha} }{rbrace} - 4 {beta_{2K}}^2 {R_2}^2 q_4 (x_0) cos alpha - 0.5 mu_{2K} }{]} delim{}{ delim{} {- {0.5 mu_{2K}}/{sin alpha} }{rbrace} - 4 {beta_{2K}}^2 {R_2}^2 q_4 (x_0) cos alpha - 0.5 mu_{2K} }{]}](/images/tech/114/math_956.5_2f8060d1e62d46786a02ca143927a740.png) ;
;
![overline{k_5} = {2 E_2 beta_{2K} R_2 d_3 q_3 (x_0) }/{E_{2K} h_{2K}} delim{[}{1 + {E_{2K} h_{2K} F_1 delim{lbrace}{R_delta - R_3 prime}{rbrace}}/{4 pi E_2 d_3 {beta_{2K}}^2 {R_2}^2 q_3 (x_0)} - {3 sin alpha}/{8 {beta_{2K}}^2 R_2 d_3 cos^2 alpha q_3 (x_0)} }{]} overline{k_5} = {2 E_2 beta_{2K} R_2 d_3 q_3 (x_0) }/{E_{2K} h_{2K}} delim{[}{1 + {E_{2K} h_{2K} F_1 delim{lbrace}{R_delta - R_3 prime}{rbrace}}/{4 pi E_2 d_3 {beta_{2K}}^2 {R_2}^2 q_3 (x_0)} - {3 sin alpha}/{8 {beta_{2K}}^2 R_2 d_3 cos^2 alpha q_3 (x_0)} }{]}](/images/tech/114/math_938_066d3d3c33c9965cee063cb6fdeefaf1.png) .
.
Коэффициент затяга фланцевого соединения крепежом
Выражение для коэффициента затяга крепежа, обеспечивающего заданное нераскрытие, получится в виде:
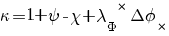 , (7)
, (7)
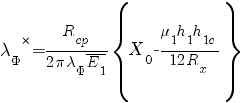 ;
;
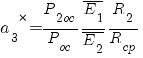 ;
;
![Delta phi_{*} = {1}/{{f_3}^{**} B^{*}} delim{lbrace}{ (k - 1 + m_1) delim{[}{1 - A_0 ( 1 + {overline{c_2} h_1 }/{2} ) }{]} - }{} Delta phi_{*} = {1}/{{f_3}^{**} B^{*}} delim{lbrace}{ (k - 1 + m_1) delim{[}{1 - A_0 ( 1 + {overline{c_2} h_1 }/{2} ) }{]} - }{}](/images/tech/114/math_951.5_e7d6aed920556f3365223dc8c13da6a1.png)
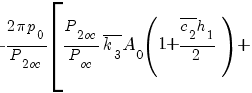
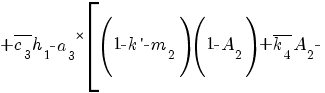
![delim{}{ delim {}{ - {2 pi p}/{P_{2oc}} delim{[}{{F_1}/{2 pi R_3} - overline{k_5} A_2}{]} }{]} }{rbrace} delim{}{ delim {}{ - {2 pi p}/{P_{2oc}} delim{[}{{F_1}/{2 pi R_3} - overline{k_5} A_2}{]} }{]} }{rbrace}](/images/tech/114/math_951.5_d830d3226400ad40399f14992ee658fe.png) . (8)
. (8)
Другие обозначение встречались ранее или смысл их тот же, что и в несимметричных фланцевых соединениях первого и второго родов.
Коэффициент затяга, соответствующий предельной плотности, должен рассчитываться по формуле (7) при X1 = X1max.
Формулы (5)–(7) получены в предположении, что φ1 > φ2. Если в результате расчета окажется, что Δφ* < 0, то будет иметь место φ2 > φ1, это означает, что эпюра нормальных напряжений вдоль p—q соответствует эпюре на рис. 2, г.
Нормальные контактные напряжения будут в этом случае создавать момент того же направления, что и момент силы PR для фланца I и момент обратного направления для фланца II. Это учтется, если в исходных выражениях для углов поворота сечения фланцев поменять знаки на обратные, перед слагаемыми,содержащими b1. Соответствующие изменения надлежит сделать в выражениях для изгибающих моментов M0 и M2.
В соответствии со схемой деформированного состояния при φ1 < φ2 раскрытие фланцевого соединения, если оно будет, начнется снаружи (см. рис. 2, г предыдущей статьи о расчете и деформации фланцев 3-го рода). В этом случае X1 следует отсчитывать от точки q с положительным направлением к периферии вдоль радиуса к точке р. Так же будет обстоять дело с отрезком а1, т.е. в этом случае максимальные изгибные напряжения возникнут в наружных волокнах болтов, расположенных в диаметральных сечениях.
Заключение
Если повторить выкладки, связанные с выводом формулы для κ при φ1<φ2, знаки перед b1 поменяются дважды и, следовательно, в конечном счете останутся неизменными. Знаки перед слагаемыми, содержащими fc, меняются только один раз, так как в выражениях для углов поворота они не меняются. Следовательно, если Δφ*<0, то надо поступить следующим образом:
- поменять знаки на обратные перед всеми слагаемыми, содержащими fc, в выражениях для f3** и A3*.
- поставить знак минус перед фигурной скобкой в выражении (8).
Рассчитанный таким образом коэффициент κ будет соответствовать случаю, когда φ1 < φ2.
При расчете изгибающих моментов М0 и M2 при φ1 < φ2 знаки перед b1 следует сменить на обратные. Соответствующие изменения нужно сделать при расчете контактных напряжений в точках p и q.
Список литературы
- Englesson J. Welded Tubular shafts for Water Turbines // Water Power, 1965, March..
- Бугов А. У. Расчет деформаций и напряжений плотных кольцевых фланцевых соединений гидротурбин // Сб. трудов ин-та машиностроения АН СССР Проблемы прочности в машиностроении, 1962, №9... – с. 73-96 c.
- Соколов С. Н. Круглая пластинка на обобщенном упругом основании // Инж. сборник, Т. 11, 1952... – с. 82-86.
Получив доступ к данной странице, Вы автоматически принимаете Пользовательское соглашение.