Фланец под механической нагрузкой. Перемещения и деформации фланцев
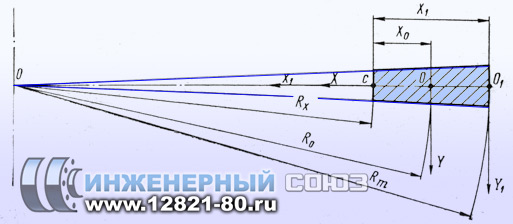
Выделение расчетного элемента фланца
Для расчета соотношений между перемещениями точек фланца и деформациями в его объеме из кольцевой детали выделяется расчетный элемент. Радиальные напряжения и деформации фланцев считаются малыми. Производится нахождение соотношений, связывающих относительные деформации кольцевых волокон фланца и относительные осевые деформации с перемещениями точек материала фланца. Эти соотношения являются нелинейными.
Дата публикации: 2 апреля 2011
Расчетный элемент фланцевого соединения
Расчетный элемент выделяется из фланцевого соединения двумя меридиональными сечениями шириной в 1 см по окружности центров отверстий для крепежа. Сечение расчетного элемента, проходящее через О1—с (рис. 1, б) показано на рис. 1, в.
Начало координат XOZ (рис. 1, б и 3) совмещено с точкой пересечения недеформированной оси расчетного элемента с плоскостью разъема. Ось OX (рис. 1, в) лежит в плоскости разъема. Направление по радиусу к оси фланца принимается за положительное направление этой оси. Положительное направление оси OZ показано на рис. 1, б и на рис. 3.

Рис. 1. Характер деформации фланцевого соединения
Следствия предположения о малости радиальных напряжений
В соответствии с принятым допущением о малости радиальных напряжений следует принять, что осевые волокна а1 – а1, б1 – б1, в1– в1, г1– г1 и другие (рис. 1, б) не давят друг на друга. Тогда радиальные перемещения точек, расположенных на образующих а1—ж 1 фланцев I и II и других конических поверхностей, будут равны между собой. Поэтому для определения радиального перемещения точек сечения фланца достаточно определить прогиб оси О2—О3 (рис. 3) расчетного элемента и поступательное радиальное перемещение сечения вследствие воздействия на фланец равномерно распределенных радиальных сил. Выражение для прогиба оси O2—O4 в точке 1 будет
u1(z) = κ1(Z2 — c12) / 2, (а)
где κ = 1/ρ1 — кривизна оси O2—O4 [ρ1 — радиус кривизны (рис. 3, а)]; u1* = — κ1c12/2 — прогиб оси O2—O4 в точке O4 в системе координат XOZ (рис. 3, а); с1— ордината оси О1 – x1, через которую проходит нейтральная плоскость нераскрывающегося участка pql1k1p фланца (рис. 3, б).

Рис. 2. Расчетная схема фланцевого соединения.
На раскрытом участке qq'e'l1q (на рис. 3, б этот участок показан штриховыми линиями) нейтральная плоскость фланца проходит через ось O'1—Х'1.Через ρ2 обозначен радиус кривизны оси O3—O4, а через R0 (рис. 1, б и 3,а) — радиус окружности, проходящей через центр тяжести О стыкового сечения расчетного элемента; Х0— абсцисса точки с,с которой начинается раскрытие, в центральной системе координат XOY (рис. 1, в); через φ1 и φ2 обозначены углы поворота торцевых образующих фланцев / и //.
Для перемещения точек оси O3—O4, расположенных выше оси ОХ (рис. 3, а), может быть написано выражение, аналогичное формуле (а). Расчетный элемент выделен из кольцевой детали. Поэтому перемещению точек расчетного элемента препятствуют кольцевые связи. Наличие этих связей будет учитываться при определении кривизны κ1 деформированной оси.

Рис. 3. К выводу соотношений между перемещениями и
деформациями в объеме фланцев
Формула (а) полностью не определяет радиального перемещения точки 1, принадлежащей фланцу, так как начало координат XOZ (рис. 3) и все точки сечения перемещаются по направлению оси ОХ в связи с тем, что кольцевые волокна фланцев I и II деформируются под воздействием равномерно распределенных поперечных сил Q0 и Q01 и внутренних давлений р0 и р. Обозначим радиальные перемещения точек сечения фланца /, вызванные этими силами, через u0. Тогда, принимая перемещение по радиусу от оси фланца за положительное, можно записать выражение для относительной деформации кольцевых волокон фланца I в виде
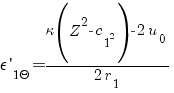 , (1)
, (1)
где r1 – радиус рассматриваемого кругового волокна фланца I, который может изменяться от наружного Rm до внутреннего Rx радиусов площади прилегания фланцев. Выражение для относительной деформации кольцевых волокон, проходящих через часть qq'e1l1q (рис. 3, б) сечения фланца /, может быть записано для сечения кольца в виде
 , (1а)
, (1а)
где r1 — радиус рассматриваемого кругового волокна фланца /, который может изменяться от Rx до RB.
Аналогичные формулы можно получить для деформации фланца //.
Относительные продольные деформации и продольные перемещения точек объема фланца
Для вывода выражения, связывающего относительные продольные деформации ez с продольными перемещениями, рассмотрим кинематику деформации расчетного элемента в следующей последовательности.
Пусть сжимающая сила Тx соответствует определенной величине усилия предварительного затяга болта Т и приложена в центре тяжести поперечного сечения расчетного элемента (рис. 1, а). Если сжимающая сила Тx приложена не по центру тяжести расчетного элемента, то эффект от эксцентрического (внецентренного) сжатия может рассматриваться как суммарный эффект от центрального сжатия и изгиба. В этом случае изгибающий момент, возникающий от эксцентрического приложения сжимающей силы, должен суммироваться с моментом внешних сил, действующих на фланец.
Пусть Δl0ф — средняя величина осевой деформации фланцев, которая возникает в результате затяга болтов. Тогда можно записать
Δl0ф = — λ'фT1 (б)
где λ'ф — податливость расчетного элемента фланцевого соединения.
Приложение осевых усилий к конструкции фланцев
Предположим далее, что к конструкции приложено осевое усилие Р∞,передающееся к расчетному элементу через оболочку в виде сил Р и Рх, приложенных не по центру тяжести расчетного элемента.
От оболочки к фланцу I будут передаваться краевые усилия М0 и Q0, величины которых, как упоминалось выше, будут зависеть от угла поворота φ1 радиальной образующей n—m фланца I и радиального перемещения точки сопряжения сечений фланца и оболочки.
По радиальной образующей фланца II n1—mх возникнут неизвестные краевые усилия М01и Qo1 как результат взаимодействия фланца II и примыкающей к нему оболочки.
Перемещения точек фланца без учета перерезывающих сил
Отвлечемся временно от перемещений всех точек меридионального сечения в радиальном направлении, вызванных перерезывающими силами. Тогда перемещение радиальной образующей а—ж вследствие внецентренного приложения сил Р и Р1 к расчетному элементу можно разложить на поступательное вдоль оси О—О (рис. 1, а) и поворот (рис. 1, б) вокруг точки, расположенной на линии а1—ж1 или на ее продолжении. Таким же образом можно представить перемещение радиальной образующей а—ж фланца II.
Будем считать, что средние деформации растяжения деформируемого объема фланцев и болтов, возникающие вследствие осевого приложения нагрузок Р,одинаковы и равны (рис. 1, а)
Δlσ = Δl1σ + Δl2σ = λσ χ Р0С, (в)
где Δl1σ, Δl2σ — осевые деформации болтов в пределах фланцев I и II, вызванные осевой силой Рос, условно отнесенной к длине окружности, проходящей через центр тяжести сечения расчетного элемента; λσ — податливость системы болтов, подсчитываемая учетом податливости всех элементов этой системы. Коэффициент основной нагрузки χ, определяющий ту часть нагрузки, которая приходится на болты (или шпильки), равен

де α' — коэффициент, зависящий от характера приложения нагрузки на фланцевое соединение.
Деформация изгиба произвольного осевого волокна
Выражение для деформации изгиба произвольного осевого волокна воротникового фланца г1—г1 может быть получено в соответствии с гипотезой конических поверхностей. Для этого нужно знать положение точек, вокруг которых происходит поворот образующих а1—ж1 и а1—ж1 и величины углов поворота этих образующих (рис. 1, б).
Если принять, что в результате центрального приложения сил Р к расчетному элементу стык не раскрывается, что имеет место почти во всех соединениях, то точки, вокруг которых происходит поворот образующих а1—ж1 и а1—ж1, будут являться точками пересечения этих образующих и осевого волокна, проходящего через центр тяжести стыкового сечения расчетного элемента длиной Х1. Таким осевым волокном для случая, изображенного на рис. 1, б, является в1—в1, которое в данном случае является осевой линией. При большем раскрытии стыка осевое волокно будет перемещаться к периферийному волокну а1—а1. Относительная деформация изгиба волокна г1—г1, отстоящего от осевой линии на расстоянии X, будет равна
 , (д)
, (д)
Предполагая, что деформация осевых волокон равномерна вдоль оси OZ,выражение для относительных осевых деформаций еz можно записать, используя формулы (б), (в) и (д), в виде
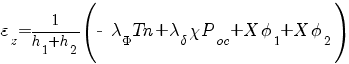 , (е)
, (е)
Используя понятие коэффициента затяга и обозначив
h1c= h1+ h2,
получим
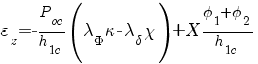 , (2)
, (2)
Заключение
Полученные приближенные соотношения (1) и (2), устанавливающие зависимость между деформациями и перемещениями, являются нелинейными, поскольку, как будет показано ниже, углы φi где i = 1, 2, являются нелинейными функциями внешних нагрузок.
Соотношение (2) является условием сплошности осевых деформаций фланцевого соединения и условием совместности, при соблюдении которого возможно определение осевых деформаций соединения по компонентам перемещений. Оно в дальнейшем может использоваться для двух целей:
- для вывода соотношения между коэффициентом затяга κ и зависящим от внешних нагрузок отрезком Х1отделяющим зону плотного прилегания фланцевого соединения от раскрытой (рис. 1, б и 2, а);
- для вывода формул по определению суммарных напряжений в болтах и на нераскрытом участке фланцев.
Кроме того, соотношение (2) устанавливает зависимость между важнейшими факторами, используемыми в теории, расчета предварительно напряженных болтовых соединений: податливостями фланцев и болтов, коэффициентами основной нагрузки и затяга фланцевого соединения. Это существенно, поскольку позволяет строить теорию расчета рассматриваемых конструкций деталей трубопроводов, используя современные достижения теории расчета предварительно напряженных резьбовых соединений.
Список литературы
- Биргер И. А., Иосилевич Г. Б. Резьбовые и фланцевые соединения.. – М.: Машиностроение, 1990. – 368 c. – ISBN 5-217-00834-2.
- Волошин А. А. Расчет фланцевых соединений трубопроводов и сосудов.. – Л. : Судпромгиз, 1959. – 365 c.
- Бугов А. У. Инженерный методы расчета симметричных кольцевых фланцевых соединений гидротурбин // Энергомашиностроение, 1970, №10... – с. 5-7.
Получив доступ к данной странице, Вы автоматически принимаете Пользовательское соглашение.